Patterns for designing algorithms

These are some patterns commonly occuring while designing algorithms. While, you may primarily devise algorithms to solve technical coding problems for your software interview, they are quite useful in real life as well. Thus, for each question I’ve not only included links to Leetcode questions but also references to real life applications. Also, this is a living document and would keep getting updated.

Sliding window

When you want to maintain a characteristic while looping through an array. For eg. In the longest substring without repeating characters problem, we maintain two pointers i and j which form the sliding window. We maintain the characteristic that the substring between i and j does not contain repeating characters. We keep moving j(right pointer) until we find a repeating character. Then we move i(left pointer) until the substring between i and j does not contain repeating characters. This is the general idea of sliding window.

Problems

• Minimum size subarray sum
• Fruits into baskets
• Longest substring without repeating characters

Binary Search

Definitions

• Problem: A statement which needs to be true for the solution. i.e. The element is the maximum of all the elements or it is a peak element or it is the first bad version.
• Search space: In binary search we have two pointers low and high(some might prefer left and right). This represent the search space where we search for the solution
• Solution: The element in our search space which solves the problem.

Loop invariants

For a binary search algorithm we generally need to prove two loop invariants.

• For each iteration, the search space always contains a solution.
• The search space reduces on each iteration, finally to only include the elements which can be a solution
  • At each step of iteration you should reduce the search space to only include the elements which can be a solution
  • The termination of loop can be proved when the search space is reduced to a single element which is the solution.

Real-life application

Git bisect

git bisect is a widely used command for identifying regression bugs. You specify a bad commit (typically the current branch’s tip) with the bug and a good commit from the past without the bug. The command then conducts a binary search, guiding you to the midpoint of the specified commits. You confirm whether the midpoint commit is good or bad, informing git accordingly. This reduces the search space through binary search, and the process repeats until the bug’s introduction commit is pinpointed.

Dynamic programming

Definitions

• memo: Any data structure, dictionary,map,array,matrix, which stores results of previously computed values to use later.

Steps for solving with dynamic programming.

The ideas here are derived from MIT 6.006 lectures

• Define subproblem. Eg. I’m taking the example for text justification shown in the lectures. We define dp(i) as the minimum badness for the text starting after word i. DP problems can be solved iteratively as well as recursively. Doing recursive DP is top-down and iterative is bottom-up. In the lectures dp(i) is used when recursive approach (or dp[i] when doing bottom up iterative approach).
• Guess and break the current subproblem in such a way that it stays in the same structure of original subproblem. Eg. We guess that breaking at j is the best choice. But we don’t blindly trust the guess and find min(badness(i,j) + dp(j)) for all j ranging from i+1 to n. This is the brute force part.
• When you are doing recursive DP you are building top down recursive tree. Notice that, to know dp(i) we call dp(j). We can say dp(i) is the parent of dp(j) for all j ranging from i+1 to n. You can visualize such a recurrence relation as shown in the diagram, in the tips section below.
• We also need to check for base cases to ensure program termination. Eg. dp(n) can be calculated as badness(n, n) which forms the base case.
• We also need to check for topological order to ensure program termination. In our example, we can clearly see that the value of i in dp(i) becomes 0,1,...n-1. Hence the topological order in which we would have answer is n, n-1, … 0(from base to top).
• Check if we solve our original problem. Our original problem here is dp(0).

Tips for dynamic programming algorithms:

• Most DP problems are optimization problems where we have to find the min or max of a property. There are problems apart from optimization where DP is useful such as calculating the total count of some property like in Fibonnaci numbers, finding if a certain proposition is true or not like in Wildcard matching.
• DP is careful brute force. Try to come up with a brute force solution and then optimize it seeing the substructure.
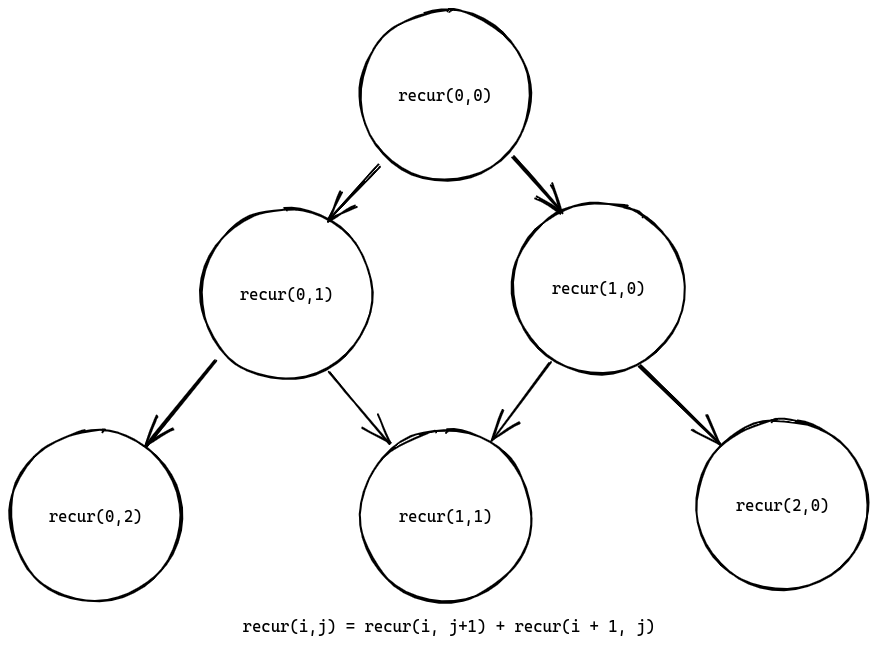
• When you are building a recursive solution and you find overlapping subproblems then you should use a memo and thus it converts to a dynamic programming problem. eg. Below is a recursive function which has a overlapping substructure. You can see that recur(0,1) and recur(1, 0) utilize the value of recur(1,1) and thus have an overlapping substructure. If a memo is not used then it needs to compute the problem again.

• Use parent pointers to reconstruct the solution as in MIT 6.006.